Two-phase flow
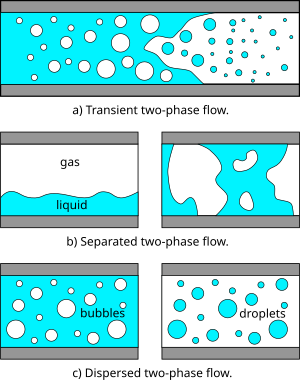
In fluid mechanics, two-phase flow is a flow of gas and liquid — a particular example of multiphase flow. Two-phase flow can occur in various forms, such as flows transitioning from pure liquid to vapor as a result of external heating, separated flows, and dispersed two-phase flows where one phase is present in the form of particles, droplets, or bubbles in a continuous carrier phase (i.e. gas or liquid).
Categorization
[edit]The widely accepted method to categorize two-phase flows is to consider the velocity of each phase as if there is not other phases available. The parameter is a hypothetical concept called Superficial velocity.
Examples and applications
[edit]Historically, probably the most commonly studied cases of two-phase flow are in large-scale power systems. Coal and gas-fired power stations used very large boilers to produce steam for use in turbines. In such cases, pressurised water is passed through heated pipes and it changes to steam as it moves through the pipe. The design of boilers requires a detailed understanding of two-phase flow heat-transfer and pressure drop behaviour, which is significantly different from the single-phase case. Even more critically, nuclear reactors use water to remove heat from the reactor core using two-phase flow. A great deal of study has been performed on the nature of two-phase flow in such cases, so that engineers can design against possible failures in pipework, loss of pressure, and so on (a loss-of-coolant accident (LOCA)).[1]
Another case where two-phase flow can occur is in pump cavitation. Here a pump is operating close to the vapor pressure of the fluid being pumped. If pressure drops further, which can happen locally near the vanes for the pump, for example, then a phase change can occur and gas will be present in the pump. Similar effects can also occur on marine propellers; wherever it occurs, it is a serious problem for designers. When the vapor bubble collapses, it can produce very large pressure spikes, which over time will cause damage on the propeller or turbine.
The above two-phase flow cases are for a single fluid occurring by itself as two different phases, such as steam and water. The term 'two-phase flow' is also applied to mixtures of different fluids having different phases, such as air and water, or oil and natural gas. Sometimes even three-phase flow is considered, such as in oil and gas pipelines where there might be a significant fraction of solids. Although oil and water are not strictly distinct phases (since they are both liquids) they are sometimes considered as a two-phase flow; and the combination of oil, gas and water (e.g. the flow from an offshore oil well) may also be considered a three-phase flow.
Other interesting areas where two-phase flow is studied includes water electrolysis,[2] climate systems such as clouds,[1] and in groundwater flow, in which the movement of water and air through the soil is studied.
Other examples of two-phase flow include bubbles, rain, waves on the sea, foam, fountains, mousse, cryogenics, and oil slicks. One final example is in the electrical explosion of metal.
Characteristics of two-phase flow
[edit]Several features make two-phase flow an interesting and challenging branch of fluid mechanics:
- Surface tension makes all dynamical problems nonlinear (see Weber number)
- In the case of air and water at standard temperature and pressure, the density of the two phases differs by a factor of about 1000. Similar differences are typical of water liquid/water vapor densities
- The sound speed changes dramatically for materials undergoing phase change, and can be orders of magnitude different. This introduces compressible effects into the problem
- The phase changes are not instantaneous, and the liquid vapor system will not necessarily be in phase equilibrium
- The change of phase means flow-induced pressure drops can cause further phase-change (e.g. water can evaporate through a valve) increasing the relative volume of the gaseous, compressible medium and increasing exit velocities, unlike single-phase incompressible flow where closing a valve would decrease exit velocities
- Can give rise to other counter-intuitive, negative resistance-type instabilities, like Ledinegg instability, geysering, chugging, relaxation instability, and flow maldistribution instabilities as examples of static instabilities, and other dynamic instabilities[3]
Additonal exhaustive information, like applied mathematical models can be found in. [4][5][6][7][8]
Acoustics
[edit]Gurgling is a characteristic sound made by unstable two-phase fluid flow, for example, as liquid is poured from a bottle, or during gargling.
See also
[edit]- Multiphase flow
- Buckley–Leverett equation
- Darcy's law for multiphase flow (for flow through porous media such as soil)
- Slip ratio (gas–liquid flow)
- Mass flow meter
Modelling
[edit]
Modelling of two phase flow is still under development. Known methods are
- Volume of fluid method
- Level-set method
- Front tracking by Gretar Tryggvason
- Lattice Boltzmann methods
- Smoothed-particle hydrodynamics (SPH)
References
[edit]- ^ a b Salomon Levy, Two-Phase Flow in Complex Systems, Wiley, 1999
- ^ Bisang J.M., Colli A.N. (2022). "Current and Potential Distribution in Two-Phase (Gas Evolving) Electrochemical Reactors by the Finite Volume Method". Journal of the Electrochemical Society. 169 (3): 034524. Bibcode:2022JElS..169c4524C. doi:10.1149/1945-7111/ac5d90. S2CID 247463029.
- ^ Ghiaasiaan, S. M.Two-Phase Flow, Boiling, and Condensation: In Conventional and Miniature Systems, Cambridge University Press, 2008. pg 362.
- ^ Ishi, M.; Hibiki, T. (2006). Thermo-Fluid Dynamics of Two-Phase Flow. Springer. ISBN 9780387283210.
{{cite book}}: CS1 maint: date and year (link) - ^ Peker, S. M.; Helvaci, S.S. (2008). Solid–Liquid Two Phase Flow. Elsevier. ISBN 978-0-444-52237-5.
{{cite book}}: CS1 maint: date and year (link) - ^ Gross, S.; Reusken, A. (2011). Numerical Methods for Two-phase Incompressible Flows. Springer. ISBN 978-3-642-19685-0.
{{cite book}}: CS1 maint: date and year (link) - ^ Stewart, H.B.; Wendroff, H. (1984). "Two-phase flow: models and methods". Journal of Computational Physics. 56: 363. doi:10.1016/0021-9991(84)90103-7.
- ^ Tiselj, I.; Petelin, S. (1997). "Modeling of two-phase flow with second-order accurate scheme". Journal of Computational Physics. 136 (2): 503–521. doi:10.1006/jcph.1997.5778.
